Эта заметка -- последняя из трилогии про свитер.
Хоть ее можно читать и независимо,
для понимания, о чем идет речь, я советую прочитать
первую и вторую заметки из этого цикла.
Вспомним, о чем речь
В прошлой заметке про свитер мы отказались от модели твердого
тела при описании падения свитера, и вместо этого решили учесть
крайнюю поддатливость свитера внешним механическим
воздействиям. Рассуждая, мы пришли к понятию
"мягкого вещества", одной из важнейших характеристик
которого является большое число внутренних слабо связанных
и сильно диссипативных степеней свободы. Именно так: в этом определении ничего не убавить. Уберите, к примеру,
сильную диссипативность, и получите... обыкновенную жидкость.
Вычерките слабую связь -- и от мягкости вещества не останется и следа.
Как я вкратце обрисовал в конце предыдущей заметки,
именно из-за этих микроскопических степеней свободы наш свитер
может находиться в медленном, незаметном для глаза движении,
и причем оно может длиться достаточно долго.
В течение этого времени внутри вещества энергия деформация,
накопленная в момент падения свитера на спинку стула, перераспределяется от одной ниточке к другой, передается
от одной степени свободы к другой. Пока в этом движении
не задействованы макроскопические степени свободы, нам со стороны
кажется, что свитер покоится. Однако как только в движение
придет значительная часть свитера -- мы увидим, как до сих пор
"неподвижный" свитер вдруг начал падать.
| |
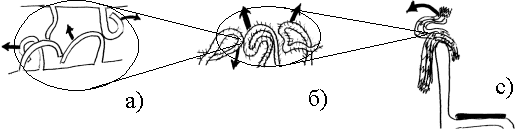
Рис.1 Схема многоступенчатой релаксации напряжений в свитере:
сначала разгибаются самые мелкие ворсинки, затем разгибаются отдельные ниточки, и наконец, это приводит в движение отдельные части всего свитера.
|
На Рис.1 я попытался проиллюстрировать это многоступенчатое
движение. На первой картинке изображен процесс распрямения
отдельных микроскопических ворсинок.
Он происходит достаточно быстро и может
привести к тому, что та ниточка, чьи ворсинки распрямились,
слегка сместится относительно соседних ниточек и сможет распрямиться
сама. Это уже не микроскопическое, а, скажем так, "миллископическое"
движение; оно показано на второй картинке.
Наконец, заметный сдвиг нескольких соседних ниточек может
привести к тому, что какая-то значительная часть всего свитера
выйдет из своего шаткого положения равновесия и придет
в движение (например, отогнется рукав, что и изображено на третьей
картинке).
Это все хорошо, но возникает резонный вопрос:
а почему мелкие ворсинки не могут просто так взять и отогнуться
и не влечь за собой вообще никаких последствий?
Откуда берется такая иерархия релаксаций,
"перетекание" энергии с микроскопического масштаба на
макроскопический?
Математически корректного ответа на этот вопрос я привести
не смогу. Однако самым главным козырем в пользу того,
что такая иерархия может происходить и скорее всего происходит,
является мое подозрение на то, что при релаксации свитера
имеет место характерное для мягкого вещества явление самоорганизованной критичности.
Самоорганизованная критичность: определения и иллюстрации
Сначала -- краткое определение.
Самоорганизованная критичность (self-organized criticality)
-- это когда система в ходе своей естественной эволюции приходит в критическое состояние. Давайте разберемся сначала
с терминами.
Что такое "критическое состояние" в физике? Это такое особое,
"безмасштабное" состояние системы, когда микроскопическое
воздействие может либо привести к таким же микроскопическим последствиям, либо вызвать макроскопическое лавинообразное переустройство всей системы. С какой-то вероятностью одно,
с какой-то -- другое. Отсюда следует вывод: в критическом состоянии
все части системы -- даже более того, все степени свободы,
пусть даже разнесенные на несколько порядков по масштабу --
тонко чувствуют друг друга: небольшие изменения одной части
системы могут отозваться на всем ее глобальном строении.
Математически, вероятность того, что в результате микроскопического
внешнего воздействия возникнет лавина размером L, имеет
степенной вид:
P(L) ~ L- alpha
где показатель alpha может оказаться как целым, так и дробным
числом (последнее чаще всего встречается в реальных системах).
Зачастую этот степенной закон тянется на несколько порядков
по L, без заметного "обрезания" на каком-либо масштабе.
Именно поэтому такое поведение называют безмасштабным.
Далее, что значит "естественная эволюция"? Это такая самопроизвольная
эволюция, для которой не требуются какие-то особенные начальные условия или параметры. Это та эволюция,
которую испытывает система, приготовленная "наобум".
То есть, систему никто никак изначально не "склонял" к критичности,
она самоорганизовалась.
| |
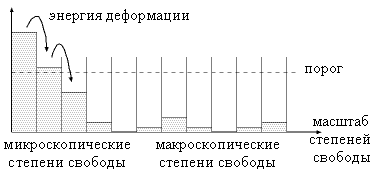
Рис.2 Схема распределения энергии деформации между
разномасштабными степенями свободы в самом начале; начинается
перетекание энергии в более крупномасштабные степени свободы --
система спонтанно эволюционирует к критическому состоянию.
|
Давайте проиллюстрируем эту эволюцию на примере того же
свитера. На рис. 2 показано распределение энергии деформации
свитера по степеням свободы (которые изображены столбиками).
Вначале у нас много энергии было запасено в "микроскопических"
степенях свободы. Потом, путем распрямления "ниточек",
часть запасенной энергии переходит к более крупным степеням
свободы. Это перераспределение энергии схематично показано стрелками.
Важно то, что у процесса перераспределения энергии есть порог
(в нашем случае за него ответственно сухое трение между отдельными
нитями). Наличие порога означает, что энергия начинает перетекать
в соседние степени свободы только, если ее концентрация в данной
степени свободы превысит какой-то определенный предел.
До тех же пор, пока это не произошло, сила трения "держит"
силу упругих деформаций.
| |
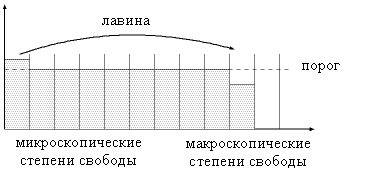
Рис.3 Структура критического состояния: все степени свободы уже переполнены, и небольшое микроскопическое воздействие по цепной реакции передается на самый крупный масштаб: возникает лавинная перестройка глобальной структуры системы.
|
Легко понять, что если существует "подпитка энергией",
то рано или поздно заполнятся все степени свободы -- как микроскопические, так и макроскопические (см. Рис. 3).
Тогда небольшая энергия, добавленная на самом мелком масштабе,
не ограничится только перетеканием в соседние степени свободы,
а сможет вызвать "цепную реакцию": степени свободы на все больших
и больших масштабах не могут удержать запасенную энергию,
и передают ее вверх по лестнице масштабов. В результате
эта энергия выделяется где-то на самом крупном масштабе
и может привести к глобальной перестройке системы.
Схематично такая лавина показана длинной стрелкой на Рис.3.
Состояние, способное порождать такие лавины,
состояние, в котором каждая степень свободы уже почти переполнена
и вот-вот "сорвется" -- и есть критическое состояние. (На самом деле,
в описанной здесь простой одномерной и однопороговой модельке
мы получим не критическое, а сверхкритическое состояние:
это когда нет расределения лавин по размерам, а всегда возникают
макроскопические лавины. В слегка усложненных моделях
возникают, однако, самые настоящие критические состояния.)
Когда критичность появляется?
Итак, это все было объяснением терминов. Остается между тем
главный вопрос: а как доказать, что та или иная система будет
обладать свойством самоорганизованной критичности?
Забавно, но оказывается общего рецепта такого доказательства
(насколько я знаю!) пока не придумали!
И это несмотря на то, что явление самоорганизованной критичности
обнаружено и исследовано во многих системах -- от динамики
землетрясений и процесса формирования дождевых капель
в облаке до поведения человеческих сообществ.
В ходе этих исследований были, конечно, выработаны некие общие
требования к системе с самоорганизованной критичностью:
например, система должна обладать большим числом степеней
свободы с заметным разбросом по масштабу,
а также эти степени свободы должны быть сильно диссипативны.
Однако никакого математического критерия, никакого строго рецепта,
разграничивающего системы с и без самоорганизованной критичности --
нет.
Интересно, что иногда оказывалось даже, что первоначальное подозрение на критичность в некоторых системах при тщательном анализе не подтверждалось. Самым известным примером является песчаная горка,
насыпанная на ровной поверхности. Вроде бы, все мы наблюдали песчаные лавинки на склоне такой горки, поэтому можно было бы предположить, что в этой системе существует самоорганизованная
критичность. Более того, в силу своей наглядности эта система
стала классическим примером самоорганизованной критичности
и даже присутствует в оригинальных работах.
Однако более поздний анализ показал, что критичность в чистом виде
здесь не проявляется. Лавины в этой системе в самом деле существуют,
но только они не распределены по степенному закону, в предпочитают охватывать сразу всю систему. Причина этого в том, что кинетическая энергия лавины не пренебрежимо мала, или другими словами, что системы это недостаточно диссипативна.
И последнее -- самоорганизованная критичность и свитер
Ну а что же можно сказать про наш свитер?
Вроде тут тоже есть множество степеней свободы, разнесенных
на большие масштабы, и причем, благодаря трению, сильно диссипативных. Вроде бы, общий вид эволюции подходит
под ту, которая дает саморганизованную критичность.
Поэтому на основании этих наблюдений я подозреваю,
что самоогранизованная критичность может сформироваться
в процессе релаксации упавшего на спинку свитера.
Она тогда будет тем механизмом, который незаметно для наших
глаз "собирает" энергию с отдельных ворсинок и частично
передает ее крупным частям свитера. И если первоначально
свитер находился на краю зоны стабильности, этот
механизм может оказаться способным вывести его из этой зоны --
туда, где падение на пол уже неизбежно.
В такой картине, именно эта внутренняя эволюция
и есть причина аномально долгого падения свитера.
Разумеется, это только подозрение, а не доказательство.
Но это подозрение основано на физическом чутье, и потому
здесь уже стоит требовать серьезных аргументов
не для доказательства, а для опровержения. Все-таки,
нужны очень сильные доводы, чтобы утверждать ложность
физического чутья.
Мне было бы очень, очень любопытно
послушать комментарии по всей этой трилогии.
Послесловие 1
Уже после первой заметки про свитер
появились комментарии, что я-де полез в дебри и упустил очевидное
объяснение первоначального вопроса: а именно, что
свитер падает из-за незаметных глазу внешних толчков и вибраций.
Да, безусловно, вибрации тоже могут приводить к "затянувшемуся"
падению свитера. Но суть моей трилогии -- показать, что
внешнее воздействие не есть необходимый фактор.
Свитер -- это такая интересная система, которая может
долгое время жить внутренней жизнью. И тогда падение свитера --
это не "вдруг", а закономерный результат его релаксации.
Послесловие 2
Я не пытался дать в этой заметке исчерпывающее объяснение
самоорганизованной критичности. Я рассказывал про нее ровно
столько, сколько мне показалось нужным для объяснения динамики
свитера. Но поскольку мне неизвестно хорошее онлайновое популярное
введение в этот предмет, то наверно можно рекоммендовать
эту заметку (а лучше, всю трилогию) для первого прочтения.
Обозрение Игоря Иванова "Теорфизика для малышей"
�