светлый и темный солитоны
В 1952 году Энрико Ферми попросил двух молодых физиков численно решить
задачу распределения начальной моды по другим на примере колебаний 64
связных грузиков. В процессе моделирования ожидаемый результат не получился,
была лишь перекачка энергии в несколько начальных мод и происходил возврат
системы к исходному состоянию и затем повторение
процесса без установления термодинамического равновесия системы(равномерное
распределение колбательной энергии по всем грузикам). После расчетов
было установлено, что модель при уменьшении расстояний между грузиками и их
неограниченом росте переходит в уравнение, описывающее поведение
уединенной волны на воде, т.н. уравнение Кортевега-де Фриса(описывающее
модель поведения
уединенной волны в бассейне, амплитуда которой много меньше глубины бассейна
и но длинной во много раз большей глубины). В процессе вычислений было
выяснено, что случае уединенной волны
её скорость тем выше, чем выше её амплитуда и полуширина пика с увеличением
амплитуды уменьшается. Если рассмотреть две такие волны разных амплитуд(и
соответственно разных скоростей), движущиеся в одном направлении, то рано
или подно наступит момент года более высокая волна догонит более
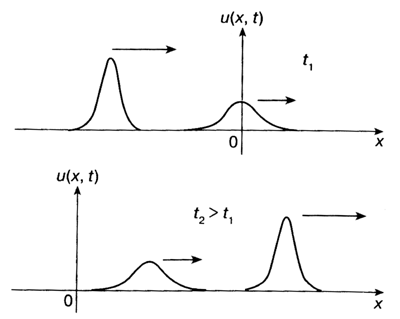
две волны до взаимодействия и после
медленную(ведь скорость движения одиночной волны тем больше, чем больше её
амплитуда). В течении некоторого времени волны будут двигаться как единое
целое и далее разъеденятся. Самым интересным свойством таких волн будет
сохранение формы и скорости после взаимодействия. Обе волны лишь немного
смещаются(приобретают фазовый сдвиг) на некоторое расстояние по сравнению с
тем случаем, когда как если бы они двигались без взаимодействия. Этот
процесс, в ходе которого при взаимодействии волн сохраняется их форма и
скорость, напоминает упругое столкновение двух частиц. Именно из-за этого
такие уединенные волны были названы солитонами(от англ. solitary -
уединенный). Уединенные волны-солитоны действительно ведут себя как частицы,
большая волна не проходит через малую при их взаимодействии. Когда уединенные
волны(солитоны) соприкасаются, то большая волна замедляется и уменьшается, а
волна, которая была малой, наоборот, ускоряется и подрастает. И когда малая
волна дорастает до размеров большой, а большая уменьшается до размеров
малой, солитоны разъединяются и больший уходит вперед. Т.е. солитоны ведут
себя подобно упругим шарикам.
Теперь определение:
Солитоном называется нелинейная уединенная волна, которая сохраняет свою
форму и скорость при собственном движении и при столкновении с себе
подобными волнами сиречь представляет собой устойчивое образование.
В природе волны как правило распространяются группами, т.е. на воде типичны
"стаи" волн. Было установлено(Дж. Фейер и Т.Бенжамен), что простая
периодическая волна на глубокой воде неустойчива и поэтому волны на
поверхности разбиваются группами. Эти данные были получены в 1967 году.
Далее в 1968 В.Е. Захаров и А. Б. Шаббат вывели уравнение, описывающее
распространение таких волн на поверхности. Это уравнение тогда уже носило
название нелинейного уравнения Шредингера и может быть решено как в виде
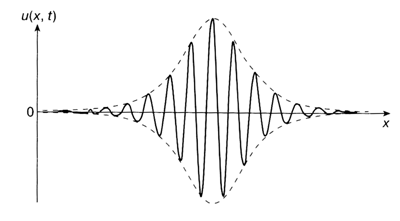
групповой солитон - огибающая группы волн
солитонов так и интегрированием методом обратной задачи рассеяния. Солитоны
из уравнения Шредингера отличаются от одиночных солитонов тем, что они
соответствуют огибающей группы волн(есть некоторое сходство с модуляцией
радиоволн). Такие солитоны называются групповыми солитонами или солитонами
огибающей. Как правило под огибающей находится 14-20 волн, причем самая
высокая волна в группе находится между седьмой и десятой(девятый вал). Если
же в группе образовалось больше волн, то произойдет их распад на несколько
групп.
До середины 60-х годов солитоном считалась одномерная волна, нынче же под
понятие солитонов попадает разнообразный спектр физических объектов от
дислокаций в кристалле(двумерные солитоны) до черных дыр в теории
гравитации.
В приведенном опыты с 64-мя грузиками неизбежно расплывание волны вследствии
дисперсии(неизбежных потерь) среды, но в то-же время волновое возмущение
изменяет среду таким образом, что свойства
среды стремятся вернуть волновое возмущение в исходное
состояние(опрокидывание нарастающего волнового фронта),
происходит своеобразная конкуренция между этими двумя процессами. При
равновеликом действии этих процессов возникает солитон, Т.е. иными словами
дисперсия и нелинейность полностью определяют форму солитона.
В оптическом случае солитоны - импульсы, сохраняющие форму огибающей при
распространении в нелинейной среде при воздействии с другими солитонами(как в
описанном выше воздействии двух волн).
В нерезонансных средах солитоны образуются в
результате баланса двух конкурирующих процессов -
дисперсионного расплывания и нелинейного самовоздействия света. Наиболее
благоприятны условия для возникрновения солитонов в одномодовых оптических
волокнах(оптических световодах) вследствии предельно малых оптических потерь и
устойчивости модовой структуры излучения при возрастании входных мощностей
вплоть до значений порога самофокусировки. Эффекты самовоздествия возникают
из-за добавки к показателю преломления небольшой величины, появляющеся
вследствии воздействия излучения на саму среду прохождения(при малой
мощности излучения происходит только частичная компенсация дифракционной
расходимости). При
распространении импульса его вершина приобретает дополнительный фазовый
набег и соответствующее этому набегу приращение к несущей частоте. И в
результате фазовой самомодуляции нарастает несущая частота от фронта
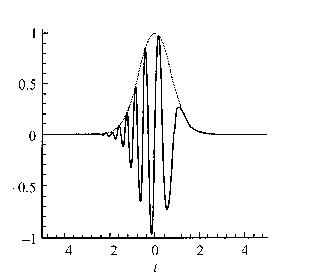
изменение частоты цуга волн
импульса к его хвосту, т.е. происходит частотная модуляция. Дисперсионное
же расплывание импульса возникает из-за дисперсии групповой скорости и
спектрально ограниченный импульс приобретает частотную модуляцию, скорость
которой зависит от пройденного расстояния. При равенстве этих процессов и
достаточной мощности вследствии уменьшения
достигаются необходимые условия для образования солитона.
Работа высокоскоростных линий связи ограничена эффектом дисперсии групповых
скоростей, из-за которого импульс уширяется, теряя энергию в битовом
промежутке. Солитоны же могут сохранять свою форму благодая балансу между
нелинейными и дисперсионными соотношениями и их использование могло бы
улучшить работу таких систем связи. Солитонные линии связи способны
передавать информацию на расстояния около 1000 км со скоростью
приближающейся к 100Гбит/с если потери в световоде скомпенсированы за счет
необходимого усиления солитонов. Например если необходимо получение линии связи на 15
Гбит/с, то усилители должны располагаться на расстоянии в 44 километра.
Длительность импульса такой системы 5,78 пс(4-фемптосекундный импульс -
Международный лазерный центр МГУ) и мощность накачки 36 мВт
соответственно.
Иными словами ставится задача увеличить пропускную способность оптоволокна на
максимально
большие расстояния. Для реализации этой задачи требуется укоротить импульс и
одновременно увеличить его мощность. В работе крымских
исследователей показано, какие параметры оптического волокна и мощности
сигнала вызывают формирование устойчивых светлых и темных солитонов.
Так-же выведено распределение плотности энергии светлого и темного солитонов
вдоль оси волокна. Волновые поверхности светлого(вверху) и темного(внизу)
солитонов представлены на рисунке в заголовке новости.
Источники:
- И.Р.Шен "Принципы нелинейной оптики" - изд-во "Наука", 1989, стр.: 474
- Г.Агравал "Нелинейная волоконная оптика" изд-во "МИР", 1996, стр.: 104
- Энциклопедия "Современное естествознание". 2001 г., "МагистрПресс", Т7, стр 188. глава "Нелинейные волны и солитоны".
- Физ. энциклопедия, 1994 г., Т4, стр 571, статья "Солитоны".
Источник: соб. информ.
�