При конструировании квантовых компьютеров
особое внимание уделяется макроскопическим
квантовым эффектам. Структуры компьютера,
основанные на этих эффектах, имеют микронные
размеры и вполне реализуемы с помощью
современной технологии. В 1999 году прогремело
сообщение об изготовлении и исследовании
квантового бита (кубита) на основе эффекта
Джозефсона [1]. В качестве кубита использовались
два зарядовых состояния: наличие или отсутствие
дополнительной куперовской пары в сегменте
джозефсоновского кольца. Строго говоря, эта
система не является идеальным кубитом, поскольку
не имеет двух собственных состояний при
одинаковых внешних условиях. Быстрое
"замешивание" этих состояний происходит только
при неадиабатическом воздействии на систему,
которое не позволяет четко контролировать
когерентность. До сих пор нет сообщений об
изготовлении двух кубитов и проведении
двухкубитных квантовых операций с ними.
Конструкция квантового компьютера,
основанного на кольцах Ааронова-Бома [2,3],
родилась в содружестве итальянских и турецких
физиков, среди которых И.О.Кулик, бывший
сотрудник Физико-технического института низких
температур в Харькове, автор одной из
основополагающих работ в области
одноэлектроники, работает сейчас в Анкаре.
Эффект Ааронова-Бома состоит в том, что
электрон, пролетающий по кольцу, помещенному во
внешнее магнитное поле, набирает дополнительную
фазу, обусловленную действием векторного
потенциала. Если посчитать магнитный поток,
пронизывающий кольцо, который обеспечивает
набег фазы 2?, то он оказывается равным кванту
магнитного потока Ааронова-Бома, равному Ф0=
hc/e. Этот квант вдвое больше кванта Абрикосова
Ф1= hc/2e для свехпроводящего
кольца или вихря просто из-за того, что заряд
куперовской пары равен двум зарядам электрона.
Если внешний магнитный поток равен целому числу
квантов Ф0, что обеспечивает наличие
конструктивной интерференции, и длина фазовой
когерентности, обусловленная рассеянием,
превосходит периметр кольца, то в нем
наблюдается так называемый незатухающий ток
(persistent current). Не то, чтобы он совсем не затухает, но
затухание может быть значительно уменьшено.
Особенно это касается случая, когда энергия
кольца с током меньше энергии кольца без тока.
Именно такую ситуацию предлагают использовать
авторы.
Устройство кубита приведено на рис.1(в заголовке новости).
Главный элемент - проводящее кольцо,
разделенное туннельными контактами на три
равных части. Кольцо пронизывает квант потока Ф1=
hc/2e, образованный вихрем Абрикосова в
сверхпроводящей фольге (S) с отверстием и
сконцентрированный ферромагнетиком (F).
Гамильтониан системы представляет собой обычный
гамильтониан, описывающий одноэлектронные
перескоки между частями кольца. Единственное
отличие состоит в том, что при этом надо
учитывать набег фазы. Низшее собственное
состояние системы является вырожденным по
орбитальному моменту ( 1 - ток по часовой стрелке
|0> и против часовой стрелки |1>). Выше по энергии
находится состояние с нулевым током |aux>,
которое является вспомогательным при проведении
операций с кубитами. Для этого используется
внешнее электрическое поле (кольцо помещено
между двумя электродами) и внешнее магнитное
поле, изменяющее магнитный поток через кольцо.
Масштаб энергий (и, следовательно, предельная
скорость выполнения операций) определяется
вероятностью туннелирования электрона между
частями кольца. Это время вполне может быть
доведено до 1пс. Температура при этом должна быть
меньше 1К. Электрическое поле, в которое помещено
кольцо, должно быть строго определенным. Иначе
вспомогательное бестоковое состояние |aux>
не опустошается при проведении операций с
кубитом (состояния |0> и |1>).
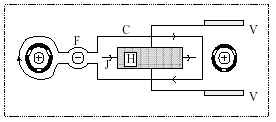 Рис. 2.
Рис. 2.
Интересно предложение по реализации
операции CNOT с двумя кубитами (рис.2). Это, как
известно, самое слабое звено в большинстве
конструкций твердотельных квантовых
компьютеров. Предлагается окружить управляющий
кубит и дополнительный компенсирующий
абрикосовский квант потока F (знак на
картинке, видимо, должен быть +) кольцом, полный
магнитный поток через который равен нулю. Кольцо
может быть сверхпроводящим. С учетом того, что в
состояниях кубита |0> и |1> собственный
магнитный поток кубитного кольца равен Ф0,
магнитное поле Н в области холловского
датчика либо наводится, либо нет. Если наводится,
то холловская эдс производит переворот
состояния управляемого кубита. В противном
случае состояние управляемого кубита не
изменяется.
Статья, по признанию и самих авторов,
"сыровата". Явно она предназначена для того,
чтобы "застолбить", вне сомнения, перспективную
идею.
- Y.Nakamura, Yu.A.Pashkin, and J.S.Tsai. Nature 398 786 (1999).
- A.Barone, T.Hakioglu, and I.O.Kulik.http://xxx.lanl.gov/abs/cond-mat/0203038
- I.O.Kulik, A.Barone, and T.Hakioglu.http://xxx.lanl.gov/abs/cond-mat/0203313
ПЕРСТ
�