|
14.08.2002
16:29 |
Солнце должно было бы схлопнуться за 40 минут! 
ГЛАВА III
ВДВОЕМ В
ОДИНОЧЕСТВЕ
Солнце, несмотря на свой огромный размер
(его радиус R = 700000 км), создает на поверхности гравитационный потенциал,
в 3600 раз больший, чем потенциал на поверхности Земли. Вспомним формулу (1)
для
потенциала точечного тела. Эта формула остается справедливой вне
сферического тела произвольного размера.
Потенциал имеет размерность энергии на единицу массы.
Такую же размерность имеет и квадрат скорости. Потенциал (конечно, по
модулю) попросту равен кинетической
энергии пробной частицы, имеющей нулевую полную
энергию. Частицы с нулевой энергией - это частицы, свободно падающие из
бесконечности. Тело, свободно падающее на Землю, имело бы скорость, равную
11 км/с на
ее поверхности, а на Солнце - 617 км/с. Квадрат их отношения примерно и
равен 3600. Превосходство Солнца
достигается за счет его массы (масса Солнца М о = 2-1030 кг; масса Земли
Mg,=6-1024 кг).
Мощные гравитационные силы стремятся сжать
Солнце. Несмотря на это Солнце не сжимается, так как
гравитационные силы уравновешиваются силами давления
газа. Это равновесие поддерживается с огромной точностью. Если бы в какой-то
момент вдруг исчезла сила
газового давления, то через 40 минут Солнце схлопнулось бы в точку. Однако
Солнце светит уже миллиарды
лет, не меняя при этом существенно своих размеров. Время схлопывания Солнца,
и вообще любой звезды, называют динамическим временем. Оно примерно равно
отношению радиуса звезды к второй космической скорости
на ее поверхности:
tд = R/Vп
(7)
Это число (40
минут) можно получить точно. Представим себе, что сила давления внутри
Солнца действительно исчезла, и оно начнет падать "само на себя". Как
долго это будет длиться? Чтобы ответить на этот
вопрос, вспомним, что
гравитационное поле вне шара совпадает с гравитационным полем точки той же
массы,
расположенной в центре шара. Тогда наша задача эквивалентна следующей:
вычислить, за какое время пробная
частица упадет на точку массы, равной массе Солнца,
с расстояния, равного радиусу Солнца. Движение такой
частицы называют свободным движением в "гравитационной воронке". Значит, оно
описывается законами Кеплера. Это движение (движение по прямой) можно
представить как движение по эллипсу, эксцентриситет которого равен единице,
а большая полуось равна половине
радиуса Солнца.
Очевидно, искомое время равно четверти периода
обращения по вырожденному эллипсу, определяемого
третьим законом
Кеплера. Подставляя
в нее Mi=M(3
и М1= массе Солнца, M2 = 0,
получимtд = 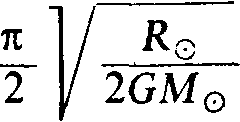 ~ 40 мин. ~ 40 мин.
Как видим,
приближенная оценка (7) не сильно отличается от точного ответа. Точность, с
которой в Солнце уравновешены силы гравитации и давления, определяется
отношением динамического времени к возрасту Солнца, т. е.
равна 10-14. Создается впечатление хрупкости Солнца. Представьте себе,
что силы давления и гравитации
разбалансировались на несколько процентов,- Солнце
схлопнется через несколько часов. Но этого не происходит. Почему?
Равновесие Солнца и звезд устойчиво. Мы знаем, что
устойчивое равновесие всегда соответствует минимуму
энергии системы. Из чего состоит энергия звезды? Она
складывается из потенциальной гравитационной энергии
и кинетической энергии частиц - ионов и электронов. Вся
кинетическая энергия большинства звезд сосредоточена
в хаотическом движении частиц (вращение, например,
Солнца, как целого дает очень малый вклад в кинетическую энергию частиц, его
составляющих. Поэтому Солнце и круглое.). Хаотическое движение частиц - это
тепловое движение, следовательно, кинетическая энергия Солнца - это его
тепловая энергия. Полная энергия Солнца
E равна сумме тепловой К и потенциальной
U энергий:
E = К
+ U .
Чтобы
проверить устойчивость звезды, давайте немного ее сожмем. На рис. 28
показана зависимость полной энергии звезды от изменения ее радиуса. Если
сжимать звезду, то тепловая энергия будет расти быстрее,
чем гравитационная падать (см.
рис. 28). Действительно, полная
тепловая энергия звезды К пропорциональна произведению массы звезды
на ее температуру: К ~
RRМТ(R - газовая
постоянная).
Будем считать, что сжатие звезды происходит достаточно быстро, так что она
не успевает отдать
тепло. Такое сжатие называется адиабатическим. При адиабатичеcком сжатии
одноатомного газа температура связана с объемом
зависимостью Т ~ V-2/3. Но объем звезды V~
R3, поэтому
T ~ R-2. И тепловая энергия при сжатии звезды растет
как 1/R2. А вот гравитационная энергия звезды пропорциональна
потенциалу, т. е. изменяется как 1/R (см. формулу (1)). График,
изображенный на рис. 28, представляет
собой сумму двух гипербол: положительной квадратичной
и отрицательной первого порядка. Минимум энергии
и соответствует равновесному радиусу звезды 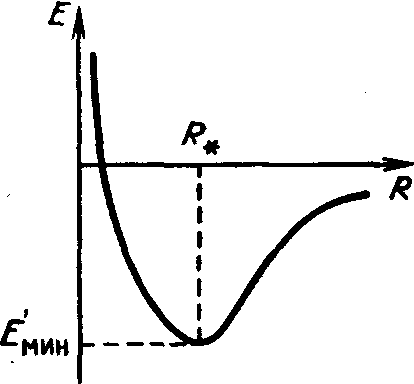
Рис. 28
Как уже
отмечалось, при сжатии звезды ее тепловая
энергия растет быстрее, чем гравитационная, следовательно, быстрее растут и
силы давления, т.е. звезда стремится расшириться. Подобно пружине, звезда
начнет колебаться вблизи равновесного значения, причем период
колебаний будет порядка ее динамического времени. Для
большинства звезд это время измеряется десятками минут или часами.
Продолжение
Обозрение "Физические явления на небесах" профессора В.М.Липунова.
�
Выскажите свое мнение на:
|