Еще в детстве я не раз подмечал такую картину: повесил я, скажем,
свитер на спинку стула, он там висит час, висит другой, а потом вдруг —
раз, и падает на пол. Причем падает безо всякого внешнего воздействия,
без толчка, в спокойной комнате, просто так — висел, висел и упал.
Или например, стоит сумка, прислоненная к стене. Стоит себе, стоит, и потом вдруг
падает. В общем, примеров вокруг меня было достаточно много, чтобы
подметить это явление.
Почему так происходит? Осознанно я этот вопрос спросил сам у себя
ближе к концу школы, и, немножко подумав, я пришел к такому
умозаключению.
Свитер, повешенный на спинку стула, находится
в неустойчивом положении (см. Рис. 1). Для простоты рассуждения
примем, что никакого трения и никаких других сил, мешающих
соскальзыванию свитера, нет. Тогда процесс его сползания
будет происходить под действием одной только силы тяжети.
| |
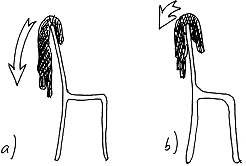
Рис.1 Свитер, соскальзывающий со спинки стула (силы трения нет).
Чем ближе к положению неустойчивого равновесия,
тем дольше будет соскальзывать свитер.
|
Если вначале свитер находился вдали от положения равновесия,
то он упадет на пол довольно быстро (Рис.1а).
Если же его поместить очень, ну очень
близко к положению равновесия, то он будет падать долго (Рис.1б).
Причем, чем ближе вначале находился свитер к положению неустойчивого
равновесия, тем дольше будет время падения.
Так что, возможно, в тех случах, когда свитер висел да висел себе два часа,
а потом упал, я его на самом деле случайно положил аномально близко
к положению равновесия, вот он пару часов, разгоняясь, "падал", а точнее, сползал.
И лишь на последней стадии, когда скорость сползания стала заметна глазом,
я увидел что свитер падает.
Такой ответ мне тогда показался правдоподобным, хотя, конечно,
то, что под действием силы тяжести свитер может разгоняться два часа,
выглядело подозрительным.
| |
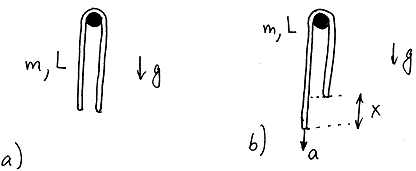
Рис.2 Моделька для падающего свитера.
Рис.2а: неустойчивое положение равновесия; Рис.2б — к решению задачи.
|
Вскоре, овладев уравнениями классической механики, я вернулся к этой задаче
и попытался решить ее. Для этого я взял известную модель: однородная цепочка
длины L перекинута через жердочку и соскальзывает под действием силы тяжести
(Рис.2). Положение равновесие, показанное на Рис. 2а, конечно же, существует,
но он неустойчиво. Действительно, если мы отойдем от него так, что разность между
концами цепочки будет равна x, то возникнет отклоняющая сила, пропорциональная x:
F = m g x/L. Эта сила приведет цепочку в движение с ускорением
a = 1/2*d2x/dt2 = F/m = gx/L.
Так что в результате мы получаем дифур, описывающий движение цепочки:
d2x/dt2 = 2gx/L.
Решение его известно: это сумма растущей и падающей экспонент.
Если в начальный момент разность между хвостами цепочки было
x0, а скорость равнялась нулю, то явный вид решения есть:
x(t) = x0/2*[ et/tau + e–t/tau], где tau = (L/2g)1/2
Когда я получил этот ответ, я понял, что мое предыдущее объяснение
того, почему свитер долго падал, никуда не годилось: быстро растущая экспонента,
появившаяся в ответе, все портит.
Действительно, можно считать, что свитер упал, когда x сравнивается с L.
Тогда если вначале свитер был достаточно близко от положения равновесия
(что нас и интересует), то вторая экспонента уже ни на что не влияет,
и время падения находится очень просто
Tпадения = tau * ln(2 L/x0)
Вся беда в том, что это время падения составляет секунды,
и его никак, ну никак не увеличить до времен порядка одного часа.
Даже если вы возьмете и положите свитер с атомной точностью
(начальное расстояние x0 не превышает размера атома), то
для L = 50 см, вы все равно получите
Tпадения = 3.5 секунды
Даже если вы улучшите точность в миллион раз (что вообще-то уже
просто физически невозможно), то время падения возрастет лишь до
Tпадения = 5.7 секунды
О каких тут часах может идти речь, если вдруг оказалось,
что невозможно заставить предмет размером с полметра падать из положения
неустойчивого равновесия хотя бы десяток секунд!
Причина этого заключения проста: как бы мы близко не подошли к положению
равновесия, страшная функция экспонента уводит нас оттуда очень и очень быстро.
Итак, та моделька явления,
которая казалась мне правдоподобной на словах, оказалась
совершенно не состоятельной, когда я попытался ее поточнее сопоставить
с реальностью. Такой вывод меня озадачил: выходит, что эта моделька
вовсе не объясняет наблюденного мною явления.
Так что вопрос остается: почему свитер висит себе и висит пару часов, а потом
вдруг падает без всякого (видимого) внешнего воздействия?
Я в следующей заметке расскажу про мое теперешнее понимание этого явления,
но пока может у кого есть какие-то идеи по этому поводу?
Игорь Иванов
�