Продолжаем разговор о двойных звездах
Ясно, что для описания орбиты нужны величины, не
зависящие от времени. Здесь на помощь
приходят законы сохранения, поскольку именно они определяют величины,
сохраняющиеся во времени.
Во-первых, сохраняется энергия двойной - система
замкнутая. Во-вторых, сохраняется полный импульс двух
звезд. В-третьих, постоянным остается вращательный
момент, связанный с орбитальным движением. Заметьте,
что нас при этом не интересуют ни размеры звезд, ни их
температуры, светимости и т. п. От этих величин движение по орбите не
зависит.
Если орбиты не круговые, появляется еще одна сохраняющая
величина - направление линии апсид.
Давайте подсчитаем, сколько величин нужно задать,
чтобы орбита была определена. Перейдем в систему отсчета, начало которой
совпадает с центром масс двойной. Момент вращения двойной - это вектор,
перпендикулярный плоскости вращения звезд. Следовательно,
задав момент вращения, мы автоматически зададим
ориентацию плоскости орбиты. Вектор задается тремя
скалярными величинами. Величина вектора не меняет ориентации плоскости, поэтому нам нужно лишь два параметра.
Однако если мы зададим
только эти две величины, мы все еще будем далеки от
полного задания орбиты. Ведь эллипс можно вращать
в этой плоскости, меняя направление большой оси (линии апсид).
Следовательно, нужно задать еще две величины, определяющие направление линии
апсид. Всего теперь будет четыре. Задав четыре величины, мы зафиксировали
орбиту в пространстве, но ничего не сказали ни о ее размерах.
Это еще одна величина. Таким
образом, всего для полного задания орбиты необходимы
5 величин. В качестве таковых, например, можно было бы задать полную
энергию двойной (одна величина),
полный вращательный момент (еще три величины), вектор в направлении линии
апсид (это еще одна величина).
Однако это не самая удачная комбинация, так как энергия
или вращательный момент прямо не наблюдаемы.
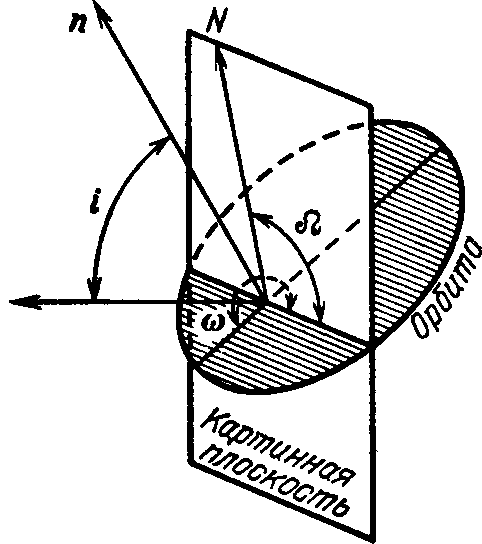
На практике пользуются следующими величинами:
большой полуосью а , эксцентриситетом
е, углом наклона i плоскости
орбиты к картинной плоскости
(т. е. к плоскости, перпендикулярной лучу зрения), углом
между линией пересечения
плоскости орбиты с картинной
плоскостью (линией узлов) и
линией апсид (долгота периастра - омега маленькое) и, наконец,
так
называемым позиционным углом Омега-большое (рис. 9). На рисунке
N указывает направление на
северный полюс мира, n - вектор нормали к плоскости орбиты. Все эти
пять параметров остаются неизменными в ньютоновской механике.
Наблюдатели двойных звезд в первую очередь стремятся определить эти пять
параметров. Но чтобы
описать движение звезд по орбите, нужно еще задать положение звезд
в какой-то условный момент и период двойной
Р (он связан
третьим законом
Кеплера через сумму масс).
Обозрение "Физические явления на небесах" профессора В.М.Липунова.
�